 POJ Founder Monthly Contest – 2007.12.30
POJ Founder Monthly Contest – 2007.12.30| Home Page | Web Board | Problems | Standing | Status | Statistics | Award Contest |
Contest -  POJ Founder Monthly Contest – 2007.12.30
POJ Founder Monthly Contest – 2007.12.30
Start time: 2007-12-30 12:00:00 End time: 2007-12-30 17:00:00
Current System Time: 2025-04-30 11:31:47.476 Contest Status:
Ended
| Problem ID | Title |
| 3472 Problem A | Holey Square Tiling |
| 3473 Problem B | Stochastic Finite State Automaton |
| 3474 Problem C | Ellipsoid |
| 3475 Problem D | Paper-, er, Transcript-Folding Game |
| 3476 Problem E | A Game with Colored Balls |
| 3477 Problem F | System of Linear Equations |
| 3478 Problem G | Undergraduate Instruction Evaluation |
| 3479 Problem H | RoBa Has a Second Art Gallery! |
[Standings] [Status] [Statistics]
| Contest Report | ||||||||||||||||||||||||
Contents
Problem A: Holey Square TilingAssuming that a horizontal domino covers the lower left corner halves the number of possible tilings. Based on this assumption, we continue to complete the tiling. First notice the case shown in Figure 1, which can be completed in only one way.  Figure 1 The remaining cases fall into two categories depending on the placement of the domino covering the upper right corner, each dividing the holey square into two isolated L-shapes (see Figure 2).
Figure 2 Apply similarly the argument of assuming a direction for the domino covering the corner to these L-shapes will further divide them into rectangles of width 2 (see Figure 3), the number of whose tilings are Fibonacci numbers.
Figure 3 Detailed discussions on counting holey square tilings can be found in [Tau04]. Problem B: Stochastic Finite State AutomatonLet fik denote the probability that the automaton is in state i after k transitions, define f(x) = xAf(x) + b or (I − xA)f(x) = b. Observe that the probability that the automaton halts in each state i is given by pi · fi(1) with Calculating expected values and standard deviations from probability-generating functions involves the derivatives of probability-generating functions. Assuming second-order differentiability of the probability generating function g(x) associated with some random variable Y, we have
(Refer to [GKP94] for further details.) It is noteworthy that for each state i, pi · fi(x) is not immediately the probability-generating function in which we are interested. The vector f(x) describes the automaton as a whole, thus each of its components reflects information about the corresponding state from the perspective of the whole automaton. For each state i, we want to find the conditional expected value and standard deviation of Xi provided that the automaton halts in state i. Consequently, the probability-generating function of interest is
This requires us to find, in addition to f(1), f'(1) and f''(1). Taking the first- and second-order derivatives on both sides of the the equation concerning f(x), we have (I − xA)f'(x) − Af(x) = 0, Again substituting 1 into all occurrences of x in the equations above we can solve for f'(1) and f''(1). Then we can easily determine the desired expected values and standard deviations. As an additional remark, the solvability of the aforementioned equations relies on the invertibility of I − A, which is ensured since I − A is diagonally dominant. Problem C: EllipsoidThe reference solution implements the principal component analysis (PCA) technique, which the author solely intends to have the problem theoretically grounded. Given a relatively loose error margin the author instead suggests that a better contest-time strategy be to figure out some subtle methods. In particular, the author finds that the following one works very well, producing results comparable to those given by PCA.
To whom may be interested, here are a brief description of how the PCA solution proceeds.
[Shl05] is a good introduction to PCA. Problem D: Paper-, er, Transcript-Folding GameThis problem is undoubtedly the easiest one of the contest. In a word, the answer is the smaller between and
Problem E: A Game with Colored BallsThe only complication of the game occurs when, after a segment is dislodged, the two segments immediately before and after the removed one share the same color and thus have to be joined into a longer one. Using a union-find algorithm we can efficiently handle the complication. All candidate segments can be maintained in a priority queue. The priority queue must support efficient modifications to its elements, since when two segments are joined, being replaced by a new, longer one and these changes have to be reflected accordingly in the priority queue. Common data structures for priority queues such as heaps and binary trees all meet this requirement. Problem F: System of Linear EquationsFor unconstrained linear system Ax = b, Gaussian elimination is an effective method. However, in the presence of nonnegativeness constraints, Gaussian elimination does not work since it has no control on the unknowns’ signs. Without loss of generality, we assume that b ≥ 0. Instead of directly seeking for a solution to the equation Ax = b subject to x ≥ 0, we alternatively starts with a solution x to the inequality Ax ≤ b subject to x ≥ 0, and strive to minimize the violation |b − Ax|1 (|·|1 means the sum of components, 1-norm, of a vector) by moving from one solution to another. Each step we try to identify an unknown xi and change its value, as well as the value of another unknown xj if necessary, abiding by the nonnegativeness constraints, so that the violation decreases. This step is repeated until the violation becomes zero or can no longer be decreased. Then we can decide whether we have discovered a solution to Ax = b subject to x ≥ 0 or the linear system has no nonnegative solution. The process above implicitly states the simplex method for linear programming applied to the problem below: minimize y1 + y2 + … + ym subject to
Problem G: Undergraduate Instruction EvaluationThe solution to this problem can be illustrated by the sample test case, which is taken from [AMO93]. The sample test case can be described as the following linear program: maximize 5y1 + 12y2 + 10y3 + 6y4 subject to
The dual of this linear program is minimize x1 + x2 + x3 + x4 + x5 subject to
which, by adding in slack variables and performing some row operations, can be rewritten as minimize x1 + x2 + x3 + x4 + x5 subject to
In this latter form, the coefficient matrix has exactly a pair of 1 and −1 in each column, coinciding with the incidence matrix of some directed network. Since the constants on the right-hand side sum to zero, the constraints can be understood as the mass balance constraints of flows. Finishing the construction, the function that is to be minimized can be considered as the flow cost. In sum, the linear program above describes an uncapacitated minimum cost flow problem. Solving the minimum cost flow problem gives a solution to the dual program. In order to find a solution to the primal program, one can establish nonnegative distance labels for the vertices with respect to the residual network. These distance labels solve the primal program and subsequently the original one. Problem H: RoBa has a Second Art Gallery![EU95] discusses this problem, the analysis in which is paraphrased as follows. It is not difficult to prove that the an optimal pair of cameras must always be installed on two vertices of the polygon. There are two different ways that two cameras can cover the whole gallery, as shown in Figure 4.
Figure 4 The case in the left is easy. However, the case in the right seems quite complicated. It is not immediately clear what choices of points C and D will minimize α + β for moving any of C and D changes α and β simultaneously. Observe that, as shown in Figure 5, taking advantage of the fact that α + β + γ + δ = 2π, we can maximize γ + δ instead. Furthermore, moving C will only change γ, and moving D will only change δ. Thus, we can maximize γ and δ independently. This last step can be done either numerically or analytically. 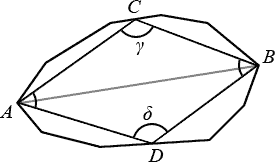 Figure 5 [EU95] proposed a quadratic time algorithm and a linear-time variant for the case where the vertices of the polygon are cocircular. References
|
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator