**以下解答主要来自出题者提供的解题报告（可能略有改动）。由于本人能力的限制，可能对于很多数据结构和算法的理解存在偏差（如果发现什么问题，十之八九不是出题者的问题，而是我自己的理解有问题，因此写得不对），欢迎大家指正。:)

Set Definition

题目所给的是个简单的双递归。我们注意到任何新的元素必然是集合中较小的元素经过两种之一的递推得到的。这启发我们两个设置标记（比如two，three两个变量）：第一个是以方式乘2加1递推，two是没有用过的最小项下标，第二则表示以乘3加1的方式递推，three是没有用过的最小项下标。开始two ＝0，three＝0，都指向最小的元素1。然后比较两种递推得到的结果，取较小的放到数组中（这样就得到了一个新的集合元素），并更新相应的下标。如果相同，只放进去一个，两个下标同时更新。这样可以线性的求出前N个元素。

Standard Point System

可以反过来考虑。首先计算标准分是x(100 <= x <= 900)的学生的成绩在所有学生中的位置，然后根据输入数据就可以知道某个学生的成绩在所有学生中的位置，从而可以知道这个学生的成绩应该换算成标准分应该处于的区间[s, s + 1)，最后根据标准分的舍入规则就可以得到某个学生最后的标准分。

Max Sequence

首先使用简单的动态规划计算A[i]和B[i](1 <= i <= N)，A[i]和B[i]分别表示从最左端到i和从最右端到i + 1的序列中，和最大子序列的值，这里计算的复杂度是O(N)。然后枚举i，A[i] + B[i]最大的值就是结果，这里的复杂度也是O(N)。因此总的复杂度为O(N)。

Treasure Exploration

构造二部图，二部图的两边都是N个结点，都分别表示原图中的点。如果从i点到j点之间存在路径，连接二部图左边的i点和右边的j点，然后进行二部图的匹配，如果得到的匹配结构是S，则需要的机器人数目是N - S。

Min-Max

本题主要考察分析转化的能力和程序设计基本功。初看起来，似乎是个很夸张的线性规划。但是50000的数据量显然不可能线性规划。实际上，本题考查的是凸包思想的运用。我们做如下考虑：建立p，q之间的对应关系，我们即得到n个整数对：(p1,q1),(p2,q2)…(pn,qn)。恰好是空间中不同的n个点。容易证明F(p1,p2…pn)＝C即是由上述n点组成的凸包中某点的横坐标，所以先求出凸包，然后求出直线x＝C与凸包的交点即可求出对应的y的取值范围：即F(q1,q2…qn)的取值范围。

Dice Stacking

本题是很经典的动态规划。开一个数组f[1<<10][10][6]，第一维表示已经用过的色子，第二维代表已经用过的色子中最后的一个，第三维代表最后的那个色子的底面。以此来表示这种状态下的最大值。

Line Segment Erase

本题主要包含两个部分：第一，求不相交区间的最大数目max。这个即是最基本的贪心模型，求出max后，用总区间数M减去max即得擦除的数目。第二部分，求不同的擦除方法总数，我们将整个关系转化成一张图：图的顶点为不同的区间，对于所给的区间Si，Sj，如果Sj能够放在Si后面而不重叠则在对应Si和Sj的顶点之间连一条有向边。于是得到一张有向图：设A为次图的邻接矩阵，令

    B ＝ A^n

Match Throwing Game

利用集合积分计算火柴和直线相交的概率。

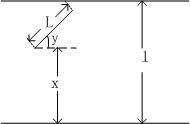
如上图，假设如果火柴和直线相交，有Lsiny >= 1 - x。计算这个区域和[0, 1] * [0, pi/2]的相交的区域（如下图）的面积和[0, 1] * [0, pi/2]区域的面积的比就是火柴和直线相交的概率p。

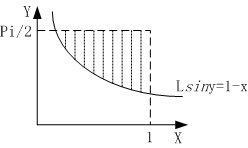
计算P = 1000 * p。这里P肯定不是整数，对P取下整。最后比较P和P + 1哪个出现的概率比较大，出现概率较大的就是最终结果。